初速度を与えて落下させる運動を「鉛直投げ下ろし運動」と呼びます。
鉛直投げ下ろし運動には、3つの有名な公式が存在するのですが、この記事では、鉛直投げ下ろし運動の3つの公式について、その意味を具体例やグラフを用いてご紹介します。

- 鉛直投げ下ろしとは?3つの公式の意味と覚え方-具体例とグラフを用いて計算方法や自由落下との違いを解説
- 自由落下と鉛直投げ下ろしの違い
- 公式①v=v0+gt は速度を求める
- 公式②y=v0t+1/2gt^2は変位を求める
- 公式③ v^2-v0^2=2gyは組み合わせ
- 等加速度直線運動の3つのグラフ
- 自宅学習ならスタディサプリがおすすめ
- 終わりに
鉛直投げ下ろしとは?3つの公式の意味と覚え方-具体例とグラフを用いて計算方法や自由落下との違いを解説
鉛直投げ下ろし運動とは、物が上から下に落ちていく運動である自由落下運動に、初速を付けた運動のことを指します。
自由落下運動が上からそっと手を放して物を落とすのに対し、鉛直投げ下ろし運動は下に向けて勢いよく物を落下させるイメージです。
加速度が一定の運動を等加速度運動と呼びますが、自由落下運動も鉛直投げ下ろし運動もこの等加速度運動の中の1つで、等加速度直線運動が横向きの運動であるのに対し、自由落下運動と鉛直投げ下ろし運動は上から下に向かって進む運動を指します。
地表において、物体が落下するときの加速度を「重力加速度」と呼び、重力加速度の値は g=9.8[m/s2] であり、この値は物体の形、大きさ、質量に依らず一定です。
この重力加速度を用いて、そっと(初速0で)物を落とした時にどのくらいの速さで落下するのかを計算したり、落下したときの移動した距離を計算できるのが自由落下の公式です。
そして、この自由落下の公式に初速度がついた公式を鉛直投げ下ろしの公式と呼びます。
鉛直投げ下ろしの3つの公式
①v=v0+gt(t秒後の速度を求める公式)
②y=v0+1/2gt^2(t秒後の変位を求める公式)
③v^2-v0^2=2gy(tが分からない時に便利な公式)
この記事では、鉛直投げ下ろしの公式について、その意味を具体例やグラフを使いながらご紹介します。
尚、等加速度直線運動のことがよくわからないという場合には、まず下記の記事を読んでから、本記事を読み進めていただくと鉛直投げ下ろしの説明がよくわかるかなと思います。
※等速直線運動についての解説はこちら
自由落下と鉛直投げ下ろしの違い
自由落下と鉛直投げ下ろしの違いは、そっと物を落とす場合(初速0の時)を自由落下、物を下に勢いをつけて落とす場合(初速が0より大きい)を鉛直投げ下ろしと呼びます。
自由落下の公式は、等加速度直線運動の公式とほぼ同じで、鉛直投げ下ろしの公式は自由落下の公式に初速度(v0)を足したものとなります。
等加速度直線運動の公式は以下の通り。
①v=v0+αt
②x=v0t+1/2αt^2
③v^2-v0^2=2αs
この3つの公式に
・初速度v0が0(手をそっと離す)
・加速度αに重力加速度 g=9.8[m/s2] (落ちるものの速度は一定)
の2つの条件をつけ足すことで自由落下の公式が完成します。
完成した公式が
公式①:v=gt
公式②:y=1/2gt^2
公式③:v^2=2gy
の3つです。尚、落下の移動方向は上から下、等加速度直線運動は左右ということで、変位の記号はxからyに代わります。これは、移動した場所が上から下なのか、左右なのかを見分けるためです。
そして、自由落下の公式に初速度(v0)を付け加えると鉛直投げ下ろしの公式となります。
①v=v0+gt(t秒後の速度を求める公式)
②y=v0t+1/2gt^2(t秒後の変位を求める公式)
③v^2-v0^2=2gy(tが分からない時に便利な公式)
このままだと意味が分かりにくいので、一つ一つの公式の意味を考えてみたいと思います。
※自由落下の公式の解説はこちら
公式①v=v0+gt は速度を求める
最初の公式は、物に初速を付けてを落としたあと、t秒たった時の速度を求める公式です。
この公式は自由落下の公式
v=gt
に初速度(v0)を付け加えて作ります。
v=gt+v0t
v=v0+gt
速度=初速度+重力加速度×時間
となりました。
続いて図を用いてイメージしてみます。

初速を付けずに静かに物を落下させると、物は毎秒9.8mの速さで加速していきます。この毎秒9.8加速することを重力加速度といいg=9.8m/s^2(^2は2乗)で表します。
重力加速度は常に一定で、重さによって落ちる速度が変わるということはないとガリレオ・ガリレイの落下の実験によって発見されました。
つまり、物を落とすと、上の図のように、1秒ごとに9.8m/sずつ落下速度が速くなっていくイメージです。
例えば、リンゴを高層ビルの屋上から自由落下させる時の10秒後の速度は
v=9.8x10
v=98m/s
となります。
この自由落下運動(そっと物を落とす)に初速度を付ける(勢いをつけて物を落とす)と、鉛直投げ下ろしの運動となります。
例えば、初速度5m/sで物が落下するとき、10秒後の速度vは何m/sとなるか。
公式に当てはめて計算すると、
v=5+9.8×10
v=103m/s
となりました。

公式①をグラフにあらわすと上のグラフのようになります。
自由落下の場合は初速度が0m/sなので、0点から始まる右上がりの直線でしたが、鉛直投げ下ろしは初速度v0から時間がたつにつれて右上がりに重力加速度分ずつ加速していくグラフとなります。
公式②y=v0t+1/2gt^2は変位を求める
2つ目の公式は変位を求める公式です。
変位というのは、その文字通り、変わった後の位置を指します。つまり移動した距離(位置)のことです。
2つ目の公式は、初速度v0で落下を始めた物体のt秒後の位置を表す公式です。
秒速1mで落下を始め、毎秒9.8m(重力加速度分)ずつ加速したときに、10秒後にたどり着く位置を計算する式だと言えます。
公式は以下の通り。
y=v0t+1/2gt^2(^2は2乗の意味)
位置=初速度x時間+1/2x重力加速度x時間x時間
それでは、この公式の意味を図を用いて確認してみたいと思います。実はこの公式は、v-tグラフというグラフを使うことでとても簡単に理解することができます。
v-tグラフって何?
先ほどの公式y=v0t+1/2αt^2の図解の前に、まずはv-tグラフって何なのか、をご紹介します。
v-tグラフは、velocity-timeグラフという名前のグラフです。速度を縦軸に、時間を横軸に記してあります。

v-tグラフを使って速度を表してみます。
速度が一定で動く場合、どれだけ時間がたっても初速度v0から速度が変化しないため、v-tグラフで表されるグラフは上のように、v0の速度がずっと続いていきます。

速度がだんだんと上がっていく場合、つまり加速度がある場合は、上のグラフのように、初速度v0から時間がたつにつれてグラフが右肩上がりに上がっていきます。
つまり、時間がたつほど速度が増しているのです。
このように、等加速度運動をグラフで表すことができるグラフをv-tグラフと呼びます。

距離を求める公式は、速度×時間でした。
速さv0m/sでt秒移動したときの距離は時間tをかけてv0×tとなります。速さ5m/sで3秒移動したときの距離は5×3=15mとなります。
v-tグラフは縦軸に速さ、横軸に時間となるので、速度v0でt秒進んだ時の位置は上の図のように、v0とtの交わる部分です。

そして、実は、先ほど計算した距離を求める公式
距離=速さ×時間
の式をv-tグラフで見ると、時間は底辺、速さは高さと考えることができ、速さ×時間で求めた距離が、上のグラフの底辺×高さと同じとなり、青色の部分の面積に等しいということが分かります。
つまり、v-tグラフを使うと、時間(底辺)×速度(高さ)で求まる面積が、移動した距離=変位=位置になるのです。
v-tグラフでy=v0t+1/2gt^2の意味を考える
v-tグラフで求まる面積が、速度vで移動t秒移動したときの位置だということが分かりました。
先ほどのv-tグラフの説明の時に少しご紹介した、加速度を表すv-tグラフをもう一度見てみます。

このグラフは、初速度v0で動いていた物体が重力加速度gの分だけ加速している状態を表しています。
つまり。速度v0で落下を始めて、9.8m/s^2ずつ加速している状態です。
速度が一定の場合にはグラフはずっと時間軸と平行だったのですが、速度が上がっていくので、グラフも右肩上がりになっていきます。
このグラフ、実は最初の公式であるv=v0+gt をグラフで表したものです。
初速度v0で進んだ位置(縦軸のv0)から、重力加速度gで加速しながらt時間分落下していった図なのです。

2つ目の公式x=v0t+1/2gt^2は、重力加速度gでt秒落ちていった時の位置を求める公式でした。
つまり、初速v0、重力加速度g、時間t で進んだ場合の位置を求めます。
この公式をv-tグラフに表してみます。
v-tグラフは、面積を求める公式である底辺×高さが、距離を求める公式の時間×速度と等しくなるグラフでした。
つまり、この上のグラフを見ると、v0で落下し続けた場合の距離をv0×tで求めることができ、v0からgだけ加速したときの距離はv0×tの上にある三角形の面積を求めることで計算できることが分かると思います。

グラフで表すと、四角の底辺の長さはtとなり、高さはv0となります。
上の三角形の底辺もtで同じです。三角形の頂点はvなのですが、vの位置はv=v0+gtです。図の右側の辺を見ると、四角形高さがv0なので、三角形の高さはv0+gt-v0でgtとなります。

あとは上の図のように、青色の四角形と赤色の三角形の面積の和を求めます。
青色の四角形の面積はt×v0=v0t…①
三角形の面積の公式は底辺×高さ÷2なので、
赤色の三角形の面積=t×gt÷2=1/2gt^2…②
①と②を足すと、
四角形+三角形=v0t+1/2gt^2となり、初速v0、重力加速度gで落下する時のt時間後の位置を求めることができました。t時間後の位置をxと表すと
y=v0t+1/2at^2となり、最初に学んだ公式を作ることができました。
尚、等加速度直線運動の変位を求める公式は「x=」の形で表すのですが、等加速度直線運動は左右の運動、鉛直投げ下ろしや自由落下は上から下への運動ということで、2つの位置を区別するために、上から下の運動の時は変位を「y=」と表します。
公式③ v^2-v0^2=2gyは組み合わせ
鉛直投げ下ろし運動の速度を求める公式と、変位(位置)を求める公式の意味が分かってきたところで、最後はこの2つの式を組み合わせることで時間(t)が分からない場合にも計算ができる便利な3つ目の公式をご紹介します。
公式は下記の通り。
v^2-v0^2=2gy
速度の二乗-初速度の二乗=2×加速度×変位
y=v0t+1/2gt^2にv=v0+gtを代入する
3つ目の公式は、時間(t)が分からない時に役立つ公式で、速度を求める公式を変位を求める公式に代入することで求めることができます。
まず、1つ目の公式と2つ目の公式がこちら。
v=v0+gt…①
y=v0t+1/2gt^2…②
3つ目の公式を作るために②に①を代入します。
最初に①の式をt=の形に直します。
v=v0+gt
gt=v-v0
t=(v-v0)/g
この式を②に代入します。
y=v0x(v-v0)/g+1/2g{(v-v0)/g^2}
この式を解いていくと、
v^2-v0^2=2gy
3つ目の公式を導き出すことができました。
公式③はどう使う?
公式①と公式②はそれぞれ速度を求めたいときと変位(位置)を求めたいときに使うので、使いどころの想像はつくのですが、公式③はどのような場面で使用するのでしょうか。
例えは、
ボールが初速度2m/sで落下を始めてから重力加速度9.8m/s^2で10m落下した時の速さを求めよ。
という問題。
この問題はわかっている数値がv0=2m/s、g=9.8m/s^2、y=10mですので、時間tが分かりません。この場合時間tを必要としない公式③を使います。
v^2-v0^2=2gy
v^2-2^2=2×9.8×10
v^2-4=196
v^2=200
v=約14.14m/s
ということで、初速2m/sで落下を始めたボールが9.8m/s^2で加速していったときに、10m進んだ状態での速度vを求めることができました。
※おすすめ物理入門書はこちら
等加速度直線運動の3つのグラフ
最後に、等加速度直線運動を考えるときに便利な、g-tグラフ、v-tグラフ、y-tグラフという3つのグラフをご紹介します。
g-tグラフ
g-tグラフは、縦軸にg(重力加速度)、横軸にt(時間)が使用されるグラフで、重力加速度gの変化量を一目で把握できるグラフです。
鉛直投げ下ろし運動というのは、重力加速度が常に一定の運動ですから、グラフのgは変化せず、下の図のようなグラフとなります。

v-tグラフ
2つ目の公式の説明に使用したv-tグラフは速度を縦軸に、時間を横軸に記してあります。物体の動きが初速度から変わらない場合は速度はv0から変化しないグラフとなりますが、加速度を持っているときは右肩上がりのグラフとなります。

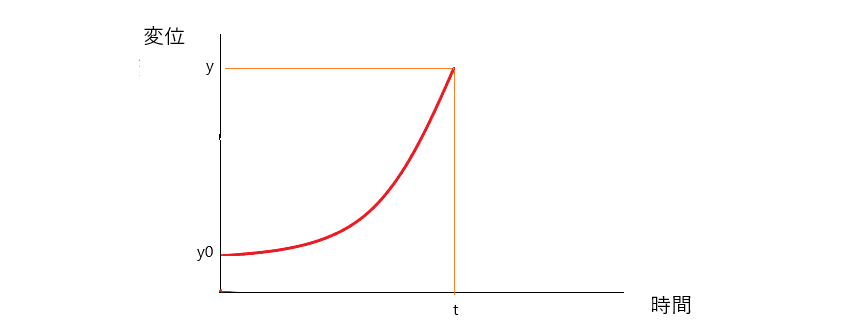
y-tグラフ
y-tグラフは縦軸に変位が、横軸に時間が記されるグラフです。
鉛直投げ下ろしの場合、時間が経つにつれて速度が増えていく(加速する)ので、進む距離も加速度分だけ大きくなります。
そのため、グラフは右上がりの曲線となります。
自宅学習ならスタディサプリがおすすめ
自宅で勉強しているけどはかどらない、学校の勉強で分からないことがある、もっと先の単元まで先取りしたいという場合には、スタディサプリ ![]() というサービスがおすすめ。
というサービスがおすすめ。
スタディサプリは『ドラゴン桜』にも登場した学習ツールで、好きな時に、自分が勉強したい単元をじっくり学ぶことができるおすすめなサービスです。
私自身、実際に使ってみて、分かりやすい授業を何度も繰り返し聞くことができ、予習復習に最適なサービスだと感じています。
スタディサプリは苦手克服にも得意を伸ばすのにもとてもおすすめですので、是非一度無料体験にチャレンジなさってみてください。
※スタディサプリホームページ
※スタディサプリの感想はこちら
終わりに
この記事では、鉛直投げ下ろし運動の3つの公式について、それぞれどういう意味なのかということを、具体例とグラフを使ってご紹介しました。
①v=v0+gt(t秒後の速度を求める公式)
②y=v0t+1/2gt^2(t秒後の変位を求める公式)
③v^2-v0^2=2gy(tが分からない時に便利な公式)
※重力加速度g=9.8m/s^2
公式を暗記するのはとても大変なのですが、公式の意味や成り立ちを理解することで、納得して公式を使うことができるようになると思いますので、是非、この3つの公式の意味を考えながら等加速度直線運の勉強を進めてみてください。
※高校生向けオンラインプログラミング教室の紹介記事はこちら
※角加速度の求め方と公式の解説はこちら
